Attention Conservation Notice My notes on a paper that builds on previous efforts to apply neural machine translation (NMT) to decompiling binaries back into human-readable source code.
They focus on compiler-specific translation pairs, which allows them to use the compiler they target to a) act as an oracle, b) generate more source-translation pairs as needed, and c) generate error-specific training samples when their decompiler makes a mistake.

Towards Neural Decompilation – Katz, et al.

I usually have a policy of not reading papers with titles in the form of “Towards [X]”, but this one came well-recommended and dovetails nicely with a lot of my interests as far as applying ML to source code and binaries. As the title suggests, it demonstrates a few clever techniques that move us further down the road to being able to train a general decompiler for arbitrary high-level/low-level language pairs.

Why would you want to do this thing?

Reverse-engineering a bit of code to figure out what it does and how it does it is a pretty common task within the security arena. It’s also difficult and time-consuming. Getting a good decompiled source code representation of a sample, rather than trying to parse out some low-level language, can help speed this process up a lot. Unfortunately, decompiling it is Hard Thing To Do[tm], and usually relies on a lot of hand-written heuristics that can be fragile. This paper aims to show that it’s possible to apply ML to the problem, and automate away a lot of the bespoke crafting of rules that is currently required for most low-level to high-level language pairs. Source code is much more structured than natural language is, as well as having a much smaller vocabulary, and easier-to-handle ambiguities, so it doesn’t seem like much of a stretch that this should be tractable at least for a wide range of high-to-low-level languages.

It’s probably worth pausing to note that “successful” decompilation, in this case, doesn’t mean “reconstruct the code as the original author wrote it”. Compilers can apply a wide range of transformations and optimizations to source code, which often make the original structure of the code unrecoverable. In this case, by “successful” decompilation, we mean that a) the recovered source code compiles, and b) the result of that compilation is functionally equivalent to the original low-level sample. But for security related tasks, that’s very often all you need; you don’t need to know how the programmer thought, you just want to know what the malware sample is actually doing to your computer.

It’s also worth noting that the authors here seem to be approaching the problem from a slightly different perspective than your usual ML paper; rather than design a general-purpose decompiler (which they do sort of end up with), their assumption seems to be that you’ve got a small set of low-level language samples that you want decompiled, and the approach they present below serves to decompile those specific samples, be you hot-starting from a pretrained NMT or no. The trained NMT model they wind up with is a happy side effect. Importantly, this means that some of their samples (they refer to them as ‘input’ samples in algorithm 1) get seen by the approach multiple times and used to generate a lot of training samples for the data; the resulting NMT model will almost certainly be biased towards those specific low-level language examples.

OK, so how do you do this?

The modeling approach itself is straightforward: they canonicalize their input (basically, they just split digits up so that numbers don’t blow out their vocabulary size) and then use an off-the-shelf NMT model (sequence-to-sequence LSTMs with attention) to generate a canonicalized version of their high-level language (basically, reorder operations into what amounts to reverse Polish notation so it’s more structurally aligned with most low-level languages). After that, they borrow techniques from program analysis: first they “decanonicalize” their canonicalized high-level sample into a template where things like numerical values are treated as placeholders, then finally work out what the actual values of those placeholders should be.

But to my mind what’s really clever is the way they exploit two facts to bootstrap their data. First, programming languages have well-defined generative grammatical structure, so they can be sampled from; you can always generate random samples of e.g. C code that are guaranteed to be valid C and compile successfully (even though they probably won’t do anything useful). Second, they have a compiler that will take any valid sample of their high-level language and produce a parallel sample in their low-level language.

Combining these two facts means that they don’t have to start with “parallel corpora” – matched pairs of high-level/low-level samples!

The “forward” direction is obvious: if you have a ton of high-level samples, and a compiler that will produce the correct low-level output from those samples, then just compile all your high-level ones to low-level ones and you’re done; there’s your parallel corpora. What really stood out to me as clever was how to generate/augment data in the “reverse” direction through exploiting the mistakes that their NMT system makes. When it generates a sample of source code that compiles, but doesn’t recover code that’s equivalent to the original low-level code, they take that high-level/low-level pair as a new data point and re-introduce it to the training data. This not only gives you more training data “for free” (since you have to generate the pairs anyway), but more training data in the region that the translation model is making mistakes.

If you wanted to make a (bad) analogy to natural language translation, this would be like having a native French speaker on hand willing to translate whatever French you gave them into English whenever you wanted, be it random French sentences from newspapers or books or whatever, or your own attempts to translate English back into French (when they’d tell you what you actually said, regardless of what you meant to say).

So that’s the general loop: you start with some samples, maybe augment them with some random ones, then compile them to make a parallel corpora. When you run your NMT decompiler, you check to see if it’s generating computationally equivalent code to the input and if it’s not, you’ve just generated a new training sample. You continue training, testing, and augmenting until you decide you’re ready to stop.

Wait, isn’t there a lot to unpack in that “computationally equivalent” line?

Yeah, actually. This bit is trickier, and I’m not sure I perfectly followed it, but the gist of it seems to be that they build a “Program Dependence Graph” (PDG) over statements in either the high- or the low-level code like the one shown below, and use two different colors of edges. One type of edge represents “data flow” – the result of some assignment or operation on a value – and the other type of edge is for “control flow” – if whether or not a particular line gets executed depends on a previous line. They then (and here’s where I’m a bit fuzzy) try to find an isomorphism between the two graphs where – once the topology matches – you also have a match between the nodes: they have the same operators or they’re both constants (they discuss variables in the paper, but I’m not sure where the distinction between that and an ‘assignment’ operator lies). Algorithm 1 suggests that they do this equivalence checking on the low-level language. This seems to make more sense to me, since low level languages tend to be more “atomic” with respect to lines (I’m imagining trying to automatically build a graph like figure 6 for something like a gnarly list comprehension/map/filter one-liner in Python), but the code listing in figure 6 is more C-like/higher-level, so I’m not sure if it’s one, the other, or both.

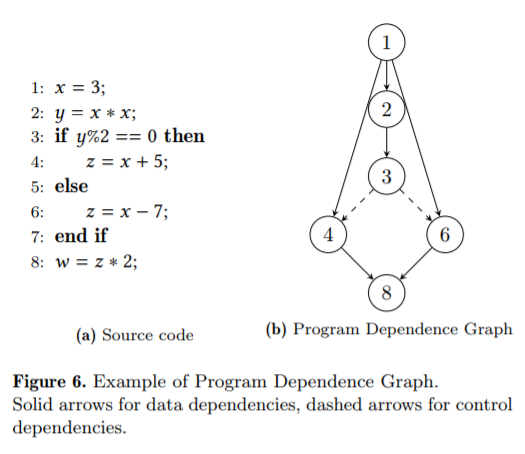
OK, so what about the “template filling”?

They start with the observation that word embeddings – as effective as they are in natural language translation – don’t work so well in machine language translation. In particular, wildly different numeric constants might be used in identical contexts; combining this with the canonicalization that they used to keep the vocabulary tractable means that embedding based models have a hell of a time figuring out exactly what number to put in which box. Variables, by contrast, are relatively easy: names don’t matter as long as they’re used in the same way, and the computational equivalence check should satisfy that. They go back to these PDGs to try to figure out the right values for constants: if there are matching nodes in a graph that are of type “constant” but have different values, then you know that that one needs to be changed, but not necessarily what the correct value is (that might depend on earlier values).

The solution to this doesn’t quite satisfy me; they use the PDG to decide which values in the predicted decompilation (\(t\), for ‘translation’) affect the numbers in the recompiled sample \(r\) you get by applying the compiler to \(t\). They do this by perturbing \(t\) and observing the effect in \(r\); after a few iterations you end up pretty confident that you’ve identified the correct value in \(t\) to change, and then… it’s heuristics. They identify a few common compiler optimizations, and basically try them all until they get a match. This seems to mostly work for them, with some exceptions noted below that seem to relate to the compiler simplifying statements.

Finally, a translation “succeeds” if they manage to make the round trip from low-level sample to high-level language back to low-level sample, where they can both get the PDGs to match up and they manage to successfully fill in the correct values using their fixes such that all constant nodes match.

Again, this process of correcting the constants – as an aside – heightens my confusion over the exact construction of the PDG: is something like cmpl 14, %eax two nodes, one for the cmpl instruction and one for the constant 14, or one node with a ‘type’ of cmpl [constant] [register] or something else entirely?

Cool! So does it work?

Yeah, basically. They get surprisingly good results over even a single iteration of Algorithm 1, using 10000 random training samples with 1000 validation and 2000 test samples. For extremely toy subgrammars of C – only assignments and unary operations permitted – they get ~100% accuracy. As they introduce binary operations, conditional flow, and finally loops and nested loops, the accuracy drops a bit, but still 70% after a single training epoch seems surprisingly high to me.

When they use the full C grammar, 6 iterations gets them to 88% accuracy. Again, this is quite good, but they note that the ‘inner’ training loop (training the actual sequence-to-sequence NMT bit, without the template construction and filling) was always terminated at 95% validation accuracy, even if it was still improving; given that the training times were relatively fast – especially considering it’s CPU-only – I’m a bit surprised that they didn’t spring for a GPU and use a more ‘generous’ early stopping criteria, such as just their ‘no improvement’ one, especially since (section 7) they implemented it in TensorFlow.

Also, surprisingly enough, they ran it single-threaded on CPU, using an AWS r5a.2xlarge, which is not super beefy as far as AWS EC2 nodes go.

What are the limitations?

Well, they main one (IMO) is that they don’t seem to have tried it on ‘real’ code samples; it would have been nice to see some brief experiments on something like the venerable Google Code Jam dataset, just to see how it did there.

It also inherits all the usual headaches of sequence-to-sequence models; longer sequences tend to perform poorly. Their template filling also has issues when multiple constants are combined to a single one, or vice versa; they give the example of x3 = 63 * (5 * x1) being converted to x3 = 315 * x1 by the compiler, whereupon the template filling approach begins to break down.

They also don’t indicate whether or not any outputs from the NMT were malformed; it’s possible that outputting it in the reverse operand order the way they do intrinsically prevents malformed/noncompilable code from being generated, either by ignoring stuff ‘left on the stack’ or some other kind of cleanup method, but if they mention that I missed it.

Conclusion?

ML on code/binaries has come a long way, and is doing some cool stuff. This paper tackles a pretty hard problem and puts a pretty creditable dent in it. The trick of exploiting the compiler to augment training data and to help fill in values in the templates is very clever. One thing that I’m really curious about is whether you could use this to do a kind of “neural transpilation” between languages – compile e.g. C code to LLVM, then “decompile” it to Rust (or whatever). I’m not sure it’d be terribly useful, but it’d be fun to see someone try it.